La fórmula general, coloquialmente llamada "chicharronera", sirve para encontrar las raíces de un polinomio de grado 2, pero ¿de dónde salio?, ¿cómo se dedujo?. Para ello primero debemos saber como es un polinomio de grado 2:
Esta es la forma estándar de un polinomio cuadrático. Como sabemos las raíces de un polinomio son los valores x para los cuales un polinomio se nulifica, es decir, se hace cero:
Cuando un polinomio tiene el valor de a=1 y se pueden encontrar dos constantes r y k tales que al sumarse dan como resultado b y al multiplicarse dan c, se puede factorizar en dos multiplicandos tales que en cada uno de ellos se tenga la variable x siendo adicionada por las constantes r y k, es decir (x+r)(x+k), cabe mencionar que tanto r como k pueden ser menores que cero, a continuación se muestra un ejemplo de lo antes expuesto:
Podemos verificar que la igualdad es cierta:
efectivamente, se cumple la igualdad. Ahora para encontrar las raíces debemos de igualar a cero el polinomio, esto por lo antes mencionado:
Recordemos que en el conjunto de los números reales si tenemos pq=0, entonces p=0 ó q=0, entonces tenemos:
Despejando:
Lo cual indica que para los valores x=-1 o x=-2 el polinomio se hace cero. Gráficamente las raíces de un polinomio son los lugares en donde la función, en este caso el polinomio, toca al eje de las x, cabe mencionar que en ocasiones las raíces pueden ser repetidas, en este caso la función sólo toca en un punto al eje x, o también existen polinomios que no tienen raíces reales, entonces se dice que tiene raíces imaginarias, en la gráfica de la función se puede observar que no se interseca en ningún punto el eje x.
Como podemos inferir, esto de factorizar no siempre es tan evidente o fácil ya que no todos los polinomios tienen como coeficiente "a" igual a uno. Para aquellos casos en los que no sea directa la factorización se utiliza la fórmula general, que deduciremos completando trinomio cuadrado perfecto al polinomio de grado dos estándar:
para encontrar las raíces primero debemos igualar a cero









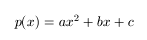

No hay comentarios.:
Publicar un comentario