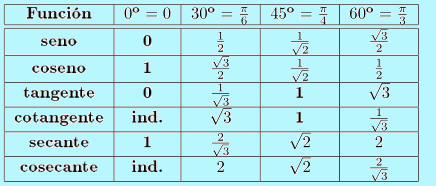
Para resolver problemas en los cuales estén involucrados ángulos, los cálculos pueden llegar a ser difíciles sin ayuda de una calculadora, pero en esta entrada se colocarán los resultados y demostración del seno, coseno y tangente de los ángulos más importantes.
Para comprobar los resultados de la tercera y quinta columna, se hará uso de un triángulo equilatero, cuyos lados tienen una unidad de longitud. Éste será dividido por la mitad, para así obtener dos triángulos rectángulos, de los cuales serán calculados las medidas que necesitamos.
El siguiente paso es calcular las razones trigonométricas del triángulo rectángulo de este esquema:
Para la cuarta columna se usará un triángulo rectángulo con ambos catetos de longitud igual a una unidad.
Pero, saber sólo las razones trigonométricas de cuatro ángulos, es muy limitado, es por ello que con ayuda de la información del seno, coseno y tangente de la suma y resta de ángulos expuesta en la entrada "Seno, coseno y tangente de suma de ángulos.", será posible deducir las siguientes razones.
Lo siguiente es deducir las razones anteriores:
En conclusión, para saber el valor de las razones trigonométricas de los ángulos más importantes, sólo es necesario recordar dos cosas; la primera es el seno, coseno y tangente de los ángulos 0°, 30°, 45° y 60°; y la segunda las fórmulas correspondientes a las razones trigonométricas de la suma de ángulos.





No hay comentarios.:
Publicar un comentario