El límite

El concepto límite se puede definir de muchas maneras dependiendo el enfoque o contexto, por ejemplo en Geografía, el límite es el lugar que indica el contorno delimitante de cierta población con atributos similares; en filosofía el concepto es muy abierto abarcando desde cuestiones ontológicas como lo son ¿A dónde nos lleva el conocimiento humano? hasta el dónde situar la delgada línea que separa lo que esta bien de lo que esta mal. Pero en lo que se enfocará este escrito es el significado de este concepto en el contexto matemático.

    El concepto de limite en matemáticas es uno de los más importantes, ya que ayuda a comprender de mejor manera algunos de los problemas más frecuentes en el análisis de una función. El significado intuitivo de limite es aproximarse lo más que sea posible a algo, y si de matemáticas es que se habla, ese algo es un valor, por ejemplo, pensemos en el número 1, si queremos acercarnos a ese valor, podemos hacerlo tanto por la"izquierda" como por la "derecha", esto claro tomando la recta real como referencia.

     

 


En este esquema se puede observar que es posible aproximarse a un punto tanto por la izquierda (valores menores al punto), como por la derecha (valores mayores).
 



    El limite de una función es uno de los conceptos más importantes dentro del cálculo, ya que sienta las bases de algunas nociones del mismo, como la derivada, la integral, continuidad, etc. La idea de limite en el cálculo se tiene que madurar, es decir, tenemos que acompañar la definición intuitiva de este concepto con ejemplos para poder tener una mejor comprensión del mismo.
    Conforme se toman valores cercanos a cierto número "a" por la izquierda o por la derecha, es posible observar el comportamiento de dicha función alrededor de la cifra "a", para entender un poco mejor lo antes mencionado, se presentan algunos ejemplos.

Ejemplo 1:
Sea f(x)=2x
Ahora se proponen valores alrededor de 3.

    En este caso en particular el límite por izquierda y por derecha es el mismo. En el ejemplo siguiente se presentará una función con límites laterales distintos alrededor de un punto dado.

    Ejemplo 2:

    

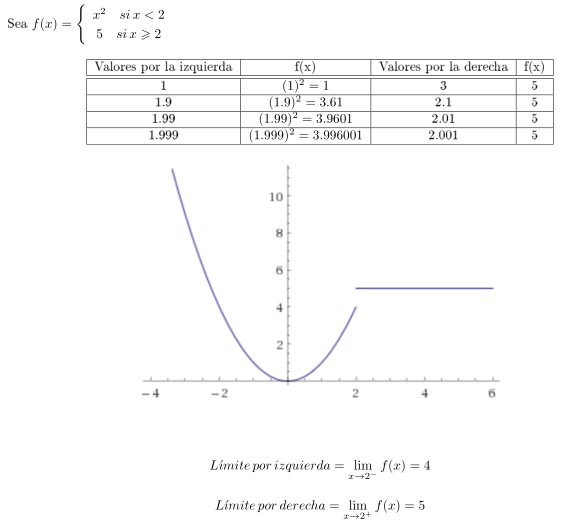
    Esta función no se aproxima al mismo valor por la izquierda que por la derecha del valor 2. En este caso se dice que no existe el límite en 2.
    Ejemplo 3:

    Este tipo de funciones además de no coincidir en sus límite laterales, conforme se acercan a cierto valor, tienden a infinito o menos infinito.
    En conclusión las funciones pueden presentarse de distinta manera, es por ello que se deben analizar de diferente forma según sea su proceder. Para llevar acabo dicho análisis, se puede hacer uso de herramientas como lo son los límites, que darán pistas del comportamiento de las funciones en ciertos puntos de su dominio.