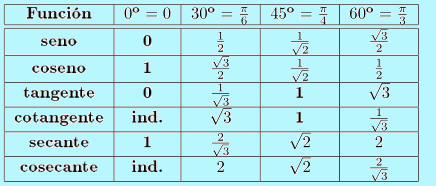
En ocasiones el estudiante se encuentra frente algún problema, en el cual se le demanda el uso de funciones trigonométricas de sumas y/o restas de ángulos. Esto puede llegar a ser un gran problema, pero si se conocen las siguientes identidades se puede salir de forma fácil y elegante de dicha problemática.
Las siguientes identidades, serán probadas para así poder ser utilizadas de forma segura:
Para la demostración, se tomará el cuadrante de los positivos del plano cartesiano y una cuarta parte de la circunferencia centrada en el origen, cuyo radio es uno. Serán trazadas dos rectas que surgirán del origen "O" y culminarán en el punto "A" y el punto "B", respectivamente en la circunferencia (líneas azul y roja), es decir su medida será una unidad de longitud. A la apertura que va del eje horizontal a la recta roja se le denominará con el nombre de ángulo x, asimismo al arco formado entre la recta azul y la roja se le llamará ángulo y. Después se tomará una recta que parta del punto "A" y termine intersectando el eje horizontal en forma perpendicular, este punto será nombrado como "C".


Lo siguiente, será tomar la misma circunferencia con las rectas azul y roja anteriormente mencionada. Ahora se trazará una recta que inicie en el punto "A" y termine tocando de forma perpendicular el segmento "OB" (línea roja), en un punto que tendrá por nombre "D". De igual manera será trazada una recta que vaya del punto "D" al eje horizontal para partirlo de forma perpendicular en un punto llamado "E".
Por último se trazarán dos rectas; una de ellas partirá del eje vertical de forma perpendicular al mismo, hasta un punto "G", pasando por "A"; el punto "G" es el lugar en el cual se forma un ángulo de noventa grados entre la recta antes descrita y una nueva línea que comienza en el punto "D". Para una mejor visualización de lo antes mencionado, se dejará un esquema señalando de color verde estos dos últimos segmentos.
De esta forma es fácil notar que se dispone de cuatro triángulos rectángulos, uno de los cuales se analizó, es por ello que en el esquema será mostrado con las medidas ya calculadas anteriormente:
Se analizarán estos triángulos de arriba hacia abajo:
Del triángulo anterior se tiene que el segmento "OD" es igual al coseno del ángulo "y", entonces:
Por ángulos complementarios la apertura entre "DG" y "DA", es igual a "x":
En resumen.
Entonces el esquema principal queda de la siguiente manera:
Como se puede observar, ya se tienen los elementos necesarios para determinar todas las fórmulas, es decir: